#필요조건 #충분조건 #역-이-대우 #귀류법
명제
정의: 참과 거짓을 객관적으로 판정할 수 있는 문장이나 식
e.g.
백두산은 한국에서 가장 높은 산 (참인 명제)
백두산은 멋있다 (거짓인 명제)
필요조건과 충분조건
명제 'P이면 Q이다' 가 참일 때
P: 충분조건 (Q이기 위한)
Q: 필요조건 (P이기 위한)
e.g. 철수는 사람이다
철수는 사람이기에 충분함 (충분조건)
철수가 되기 위해선 사람일 필요가 있다 (필요조건)
e.g. 재즈는 음악이다
재즈는 음악이기에 충분함 (충분 조건)
재즈가 되려면 음악일 필요가 있음 (필요 조건)

문제)
실수 x에 대하여 -1 < x ≤ 2인 것이 a < x < a + 4이기 위한 충분조건이 되는 a의 범위를 구하세요.
역 이 대우
P => Q 의 역 이 대우 관계
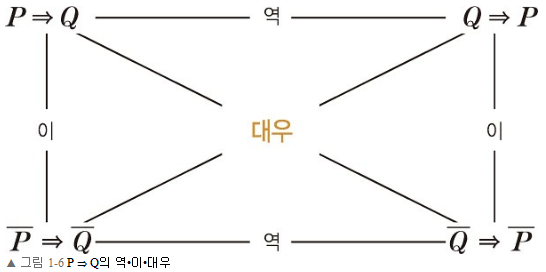
* 명제의 참-거짓은 대우의 참-거짓과 같다.
문제)
명제 ‘자연수 a, b에 대하여 a2 + b2이 홀수이면 ab는 짝수’가 성립함을 증명하세요.
귀류법
정의: 증명하려는 결론의 부정을 가정해서 모순을 끌어내는 증명법
(1) 증명하려는 결론을 부정한다.
(2) 모순을 끌어낸다.
증명이 까다롭다? 먼저 대우로 바꿔서 생각해보고 그래도 어렵다? 귀류법
* 불가능한 것, 존재하지 않을 것, 무한한 것 등을 증명하는 경우에 귀류법을 자주 사용함
(고등수학에서는 무리수 문제가 대부분... e.g. 분수로 나타내기 불가능한 숫자)
e.g.
음악이 아니다 => 재즈가 아니다
(결론 부정) 음악이 아니라는 것은 재즈라고 가정한다.
(모순 찾기) 재즈는 음악에 포함되므로 모순된다.
(증명 하기) 따라서 음악이 아닌 것은 재즈가 아니다.
문제)
x, y가 모두 홀수이고 n이 정수일 때, x, y에 대한 방정식 x2 + y2 = n2을 만족하는 (x, y)가 존재하지 않음을 증명하세요.
>> 기하학을 배우는 진짜 이유 -파스칼의 설득술-
기하학을 배우는 진짜 목적은 무엇이라고 생각하나요?
기하학을 실생활에 필요한 수학과 비교해 보면 기하학은 실용적이지 않을지도 모릅니다. 특히 도형에 관한 지식을 배우는 기하학은 사회에서는 거의 도움이 되지 않습니다. 함수와 방정식, 확률·통계에 관한 지식과 기술이라면 모를까 기하학에서 배우는 합동과 피타고라스 정리, 원주각의 정리 등을 업무나 생활 속에서 활용할 수 있는 상황은 (극히 제한된 경우를 제외하고) 일단 없다고 봅니다.
그래도 우리들은 기하학을 버리지 않습니다.
실용적이지 않지만 배우는 것 자체에 의미가 있기 때문입니다. 수학의 모든 분야에서 (장래에 수학을 사용하지 않는다면 더더욱) 기하학만큼은 반드시 배워야만 한다고 생각합니다. 서양에서 2,000년 이상 수학 교과서로 계속 사용해 온 <원론>(Digireads.com Publishing, 2017)이라는 책을 알고 계신가요? <원론>은 알렉산드리아에서 활동한 유클리드(Euclid, 기원전 330~275경)가 고대 그리스에서 기원전 6세기 이후에 발전했던 논증 기하학을 정리한 책입니다.
<원론>은 총 13권으로 이루어진 책인데, 대부분 도형에 관한 내용입니다. 그 당시에는 아직 함수나 방정식은 물론 오늘날 우리가 사용하는 수식조차 존재하지 않았기 때문입니다.
뒤집어서 생각해 보면 <원론>은 좀 더 실용적인 수학이 탄생한 이후에도 계속 수학 교육의 중심에 있었던 것입니다. 왜일까요?
그것은 논리적 사고력을 단련하는 데는 기하학을 이용하는 방법이 가장 원시적이면서도 명료하기 때문입니다.
실제로 한국의 수학 교육 과정에서도 ‘증명’은 중학교 1학년의 ‘작도와 합동’이라는 기하학 단원에서 처음 다룹니다.
사람을 설득하는 두 가지 방법
‘인간은 생각하는 갈대’라는 격언으로 널리 알려진 파스칼(Biaise Pascal, 1623-1662)은 <설득술에 대하여>라는 글 속에 사람을 설득하는 두 가지 방법을 다음과 같이 기록했습니다.
(1) 상대가 마음에 들어 하는 말투를 쓰는 방법
(2) 엄밀한 논리를 쌓아 상대를 논파하는 방법
파스칼은 대단히 뛰어난 작가이기에 (1)번 방법에도 재능이 있었지만 본인 스스로는 (1)번 방법은 서투르다며 겸손한 태도를 취했습니다. 그러고는 (2)번 방법만 파고들었다고 합니다. 다음과 같이 간단하게 정리해 둡니다.
이것이 <원론>이 전하는 논리적 사고의 기초 그 자체이며, 이 자세를 몸에 익히는 것이야말로 기하학을 배우는 진짜 이유입니다.
- 다시 고등 수학 본문 중 -
'배움 - 차근차근 기록하자 > [학습] 수학' 카테고리의 다른 글
| [대수학] 01 이차방정식 (0) | 2022.12.17 |
|---|---|
| [기하학] 03 삼각비 (1) | 2022.12.15 |
| [기하학] 02 도형의 성질 (0) | 2022.12.14 |
| [다시 고등 수학] 커리큘럼 정리 (0) | 2022.12.13 |







