#평행사변형 #삼각형의합동 #중점연결정리 #무게중심 #외심 #수심 #원주각
평행사변형의 성질
정의: 두 쌍의 마주보는 변이 각각 평행한 사각형
정리:
(1) 두 쌍의 대변의 길이가 같음
(2) 두 쌍의 대각의 크기가 같음
(3) 두 대각선의 중점에서 만남
조건:
(1) 두 쌍의 대변이 평행
(2) 두 쌍의 대변의 길이가 같음
(3) 두 쌍의 대각의 크기가 같음
(4) 한 쌍의 대변이 평행하고 길이가 같음
(5) 두 대각선의 중점에서 만남
* 삼각형의 합동 조건
(1) 세 변의 길이가 같다
(2) 두 변의 길이와 그 끼인각의 크기가 같다
(3) 한 변의 길이와 양 끝각의 크기가 같다
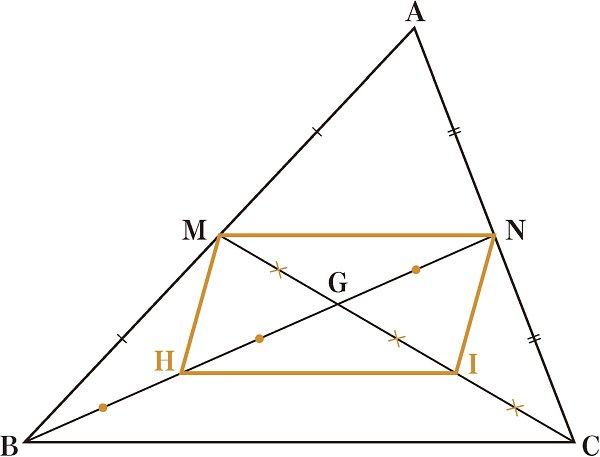
중점 연결 정리

성질:
(1) 변 MN과 변 BC는 평행
(2) 변 MN의 길이는 변 BC의 절반(1/2)
증명 : 삼각형 AMN과 닮음인 삼각형을 만들어 생각해보자.

삼각형의 오심
1. 무게중심: 3개의 중선이 만나는 점
2. 외심: 외접원의 중심
3. 내심: 내접원의 중심
4. 수심: 각각의 꼭짓점에서 대변에 내린 3개의 수선이 만나는 점
5. 방심: 한 내각을 나누는 2등분선과 다른 두 외각을 나누는 이등분선의 교점

무게중심
성질: 세 변을 2:1로 내분한다.

증명: 평행사변형을 만들어 생각해보자.
외심
성질: 외심과 각 꼭지점 사이의 거리는 같다.

증명: 선분의 수직이등분선 정리를 이용해보자.
* 선분의 수직이등분선 정리

성질: l을 선분 AB의 수직이등분선이라고 하면 다음이 성립.
(1) AP = BP ⇒ P는 l 위에 있음
(2) P가 l 위에 있다. ⇒ AP = BP
수심
성질: 삼각형의 각 꼭짓점에서 대변에 내린 수선은 한 점에서 만남
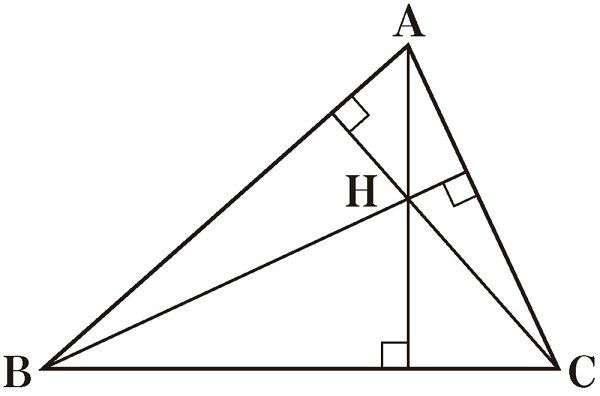
증명: 삼각형의 외심 성질을 이용해보자. (큰 삼각형)

원주각의 정리
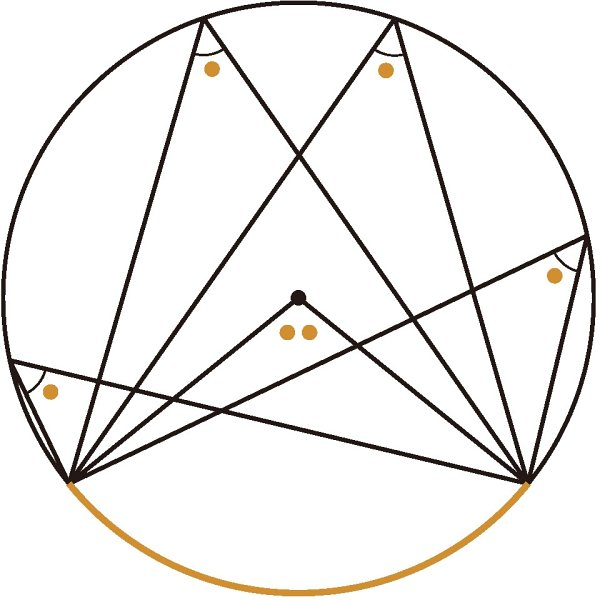
성질:
(1) 원주각의 크기는 중심각의 절반
(2) 하나의 호에 대한 원주각의 크기는 모두 같음
증명: 삼각형의 외각의 크기 성질 이용

알아 두면 편리한 ‘톨레미의 정리’
톨레미란 고대 그리스의 천문학자 프톨레마이오스(Ptolemy)를 말합니다. ‘톨레미의 정리’가 고등학교 교육 과정에 포함된 내용은 아니지만 나중에 배울 삼각함수의 덧셈정리만큼 중요하므로 소개합니다. 실제로 프톨레마이오스는 이 법칙을 바탕으로 오늘날 이야기하는 삼각비를 계산해서 행성의 운행 데이터를 수학적으로 설명하는 데 성공했습니다.
톨레미(프톨레마이오스)의 정리
원에 내접하는 사각형 ABCD에서 대변의 길이를 곱해서 더한 값은 대각선의 길이를 곱한 값과 같습니다. 즉, 다음 식이 성립합니다.

AB•CD + AD•BC = AC•BD
'배움 - 차근차근 기록하자 > [학습] 수학' 카테고리의 다른 글
| [대수학] 01 이차방정식 (0) | 2022.12.17 |
|---|---|
| [기하학] 03 삼각비 (1) | 2022.12.15 |
| [다시 고등 수학] 커리큘럼 정리 (0) | 2022.12.13 |
| [기하학] 01 명제의 증명 (0) | 2022.12.13 |







