728x90
반응형
#삼각비 #사인법칙 #코사인법칙 #헤론의공식
삼각비
* 직각삼각형의 닮음
직각이 아닌 한 각도가 서로 같은 직각 삼각형은 모두 닮음.

서로 닮음인 도형은 대응변의 길이의 비가 같음

이는 아래와 같다.
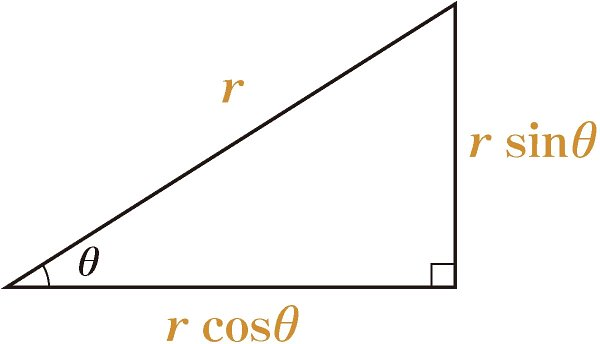

유도식 1

유도식 2

유도식 3

문제)

사인법칙

정리 : 삼각형 ABC에 외접하는 원의 반지름을 R이라 하면 아래의 공식 성립

증명: 원주각의 정리를 이용하자. (지름)
* 지름에 대한 원주각은 항상 90도 이다.
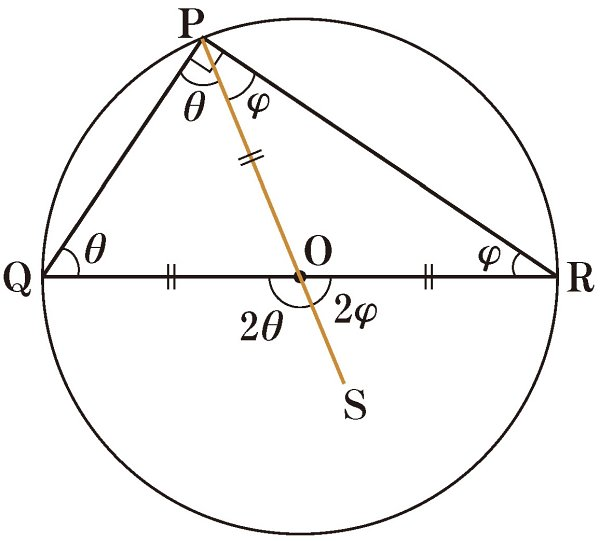
코사인법칙
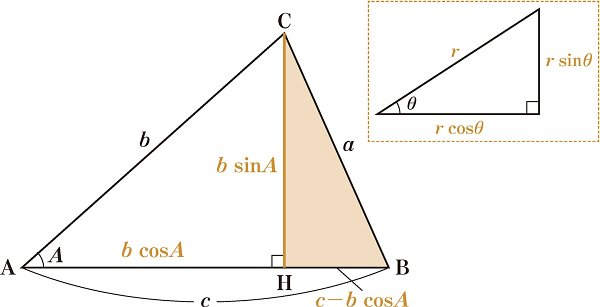
정리: 삼각형 ABC에서 다음 등식이 성립함.
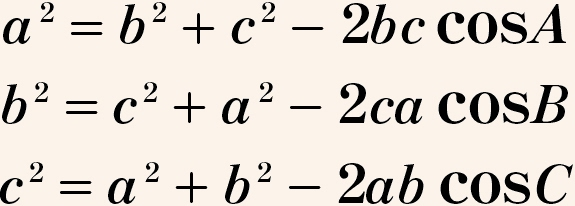
증명: 피타고라스 정리를 사용하자
문제)
∆ABC에서 a = 5, b = 6, c = 7일 때, 이 삼각형의 넓이 S를 구하세요
.
* 사인법칙은 각도의 정리, 코사인법칙은 변의 정리
문제 안에 각도에 대한 정보가 많은지, 변에 대한 정보가 많은지에 따라 사인 법칙, 코사인 법칙을 적절히 활용하자.
해론의 공식 유도하기
정리: 삼각형 ABC의 넓이를 S라고 하면 아래가 성립
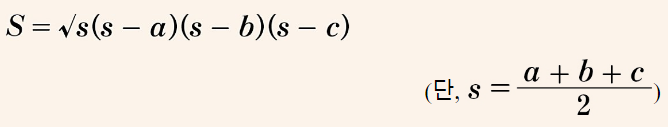
삼각형의 변의 길이만을 가지고 넓이를 구하는 공식을 일반화.
헤론은 고대 로마의 알렉산드리아(현재의 이집트)에서 활약한 그리스 사람입니다.


728x90
반응형
'배움 - 차근차근 기록하자 > [학습] 수학' 카테고리의 다른 글
| [대수학] 01 이차방정식 (0) | 2022.12.17 |
|---|---|
| [기하학] 02 도형의 성질 (0) | 2022.12.14 |
| [다시 고등 수학] 커리큘럼 정리 (0) | 2022.12.13 |
| [기하학] 01 명제의 증명 (0) | 2022.12.13 |







